Kim Geon Woo Unreal Client

삼각함수를 학습하는 이유

언리얼 엔진을 통한 클라이언트 개발 시 물체의 위치,회전,이동(Transform)과 물리 계산등 다양한 계산에 삼각함수에 대한 계산이 필요했습니다.

1. 마우스 커서가 가리키는 방향을 바라보게하려면 아크탄젠트를 사용해 각도 계산하기
2. 캐릭터나 물체를 특정 궤적을 따라 이동시키기
3. 조명, 그림자, 반사효과 등 광원의 세기 등

삼각함수

• 각의 크기를 삼각비로 나타내는 함수
• 동경의 크기에 따라 변화하는 함수
• 직각삼각형에서 각도와 변의 비율을 나타내는 함수
  • Sin,Cos,Tan
• 각도를 나타내는 방법
  • 도(Degree), 라디안(Radian)
• 주어진 함수에 대한 각을 구하는 함수
  • 역함수 (Arcsin, Arccos Arctan)
• 세변과 그에 인접한 각도 간의 관계를 나타내는 법칙.
  • 두 점간의 거리를 구할 때
  • 코사인법칙

직각삼각형을 통한 정의 Sin, Cos, Tan

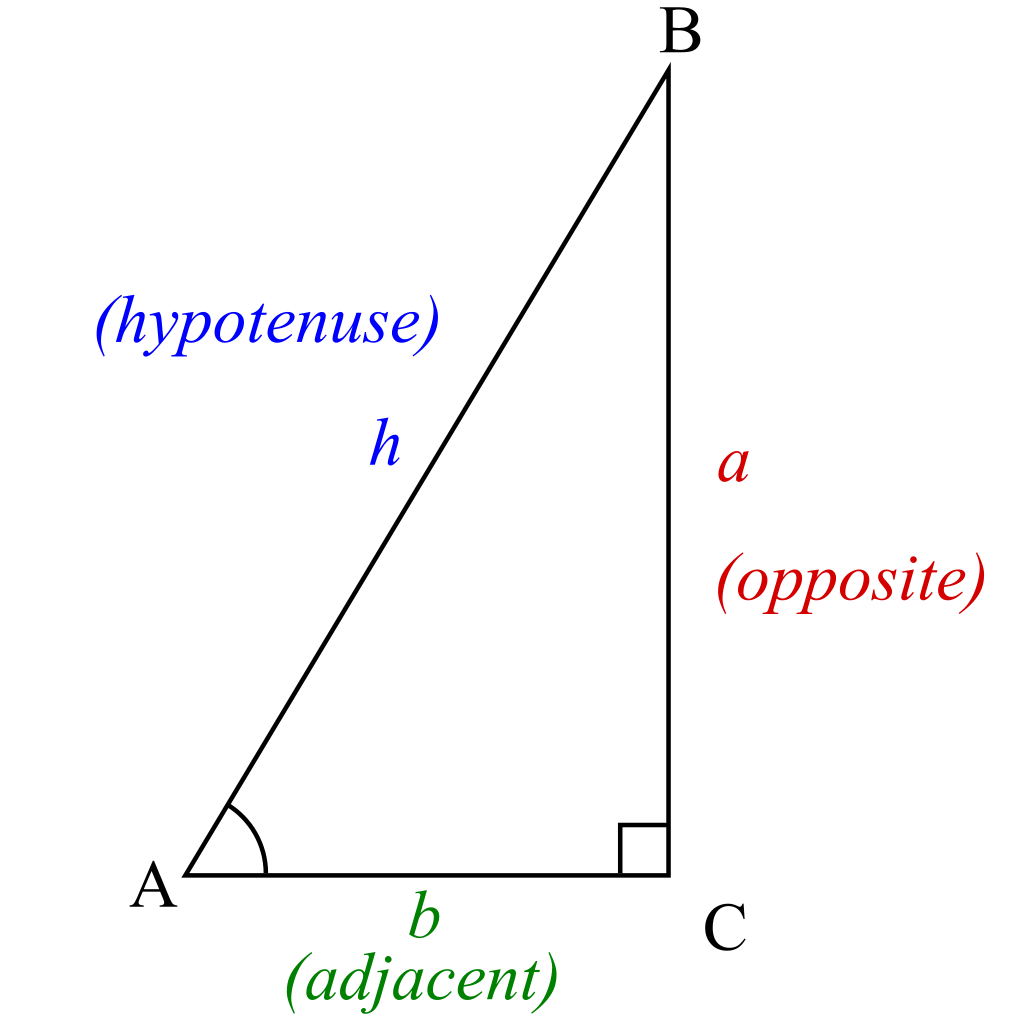
• Sine(Sin)
  • 직각삼각형에서 각의 대변과 빗변의 비율
  • y축 관련 계산에서 사용된다.
  • Sin A = a/h
• Cosine(Cos)
  • 직각삼각형에서 각 인접변의 비율
  • x축 관련 계산에서 사용된다.
  • CosA = b/h
• Tangent(Tan)
  • 각의 대변과 인접변의 비율
  • 기울기 계산에 사용된다.
  • TanA = a/b

코사인 법칙

코사인 제 1법칙

• c = b Cos A + a COS B
  • 양 변의 길이와 알고자 하는 변 사이의 두 각의 크기를 아는 경우, 다른 한변의 길이를 알아낼 때 사용할 수 있다.

코사인 제 2법칙

• b^2 = c^2 + a^2 - 2caCosB
  • 두 변의 길이와 끼인각의 크기를 알 때 삼각형의 나머지 한 변의 길이를 구할 때 쓸 수 있다.

단위원을 통한 정의 Sin θ , Cos θ , Tan θ

• 좌표 평면에서 원점을 중심으로 하고 반지름 r의 길이가 1인 원
• 점(x,y)에 대해 x축과 원점을 잇는 직선각 θ를 정의

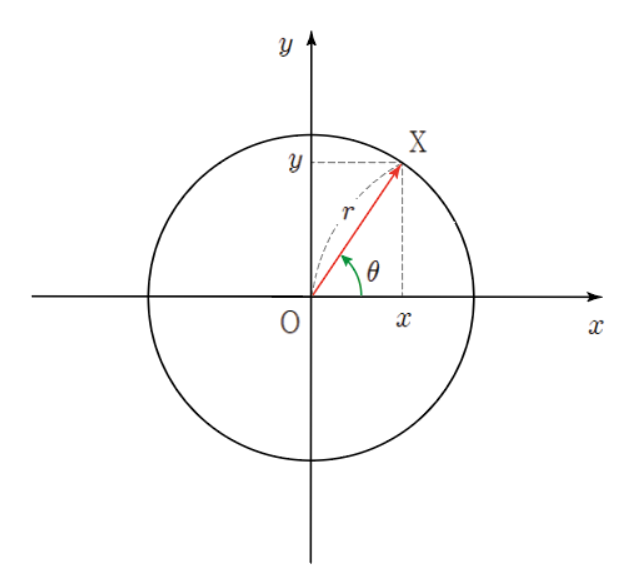
• sin θ = y/r
• cos θ = x/r
• tan θ = y/x = sin θ / cos θ

특수각

• 각 중에서도 0,30,45,60,90도와 같은 각도로 삼각비 값을 계산하거나 기억하기 쉽게 정리되 각도
• 특정한 수치로 계산된다.

호도법 Radian

• 호의 길이로 각도를 표현하는 방법
• 라디안(Radian) : 호도법으로 표현하는 각의 크기
  • 각에 대응하는 호의 길이를, 원의 반지름으로 나눈 값
  • 호의길이 = 반지름 길이, 360 = PI = 180
  • 원 위의 점이 원점을 중심으로 반지름의 길이만큼 한 방향으로 움직였을 때 대응하는 각의 크기 : 1 라디안

삼각함수 항등식

• 삼각함수가 나오는 항등식

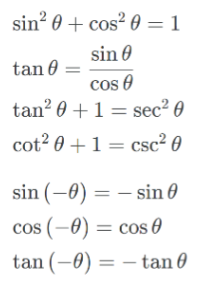
Sin Cos 그래프

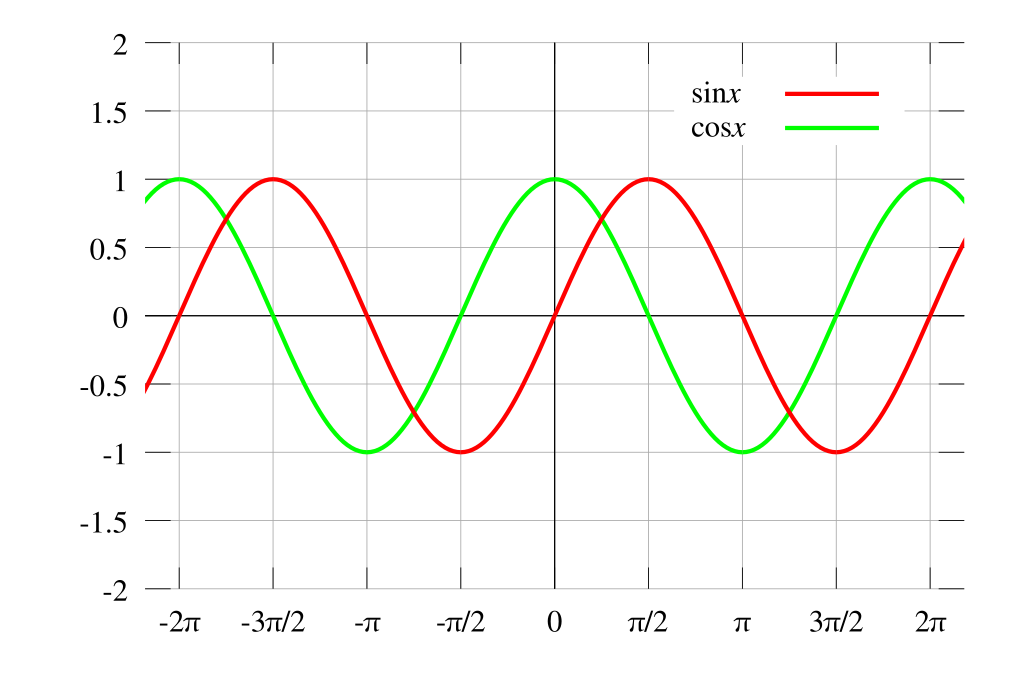
Tan 그래프

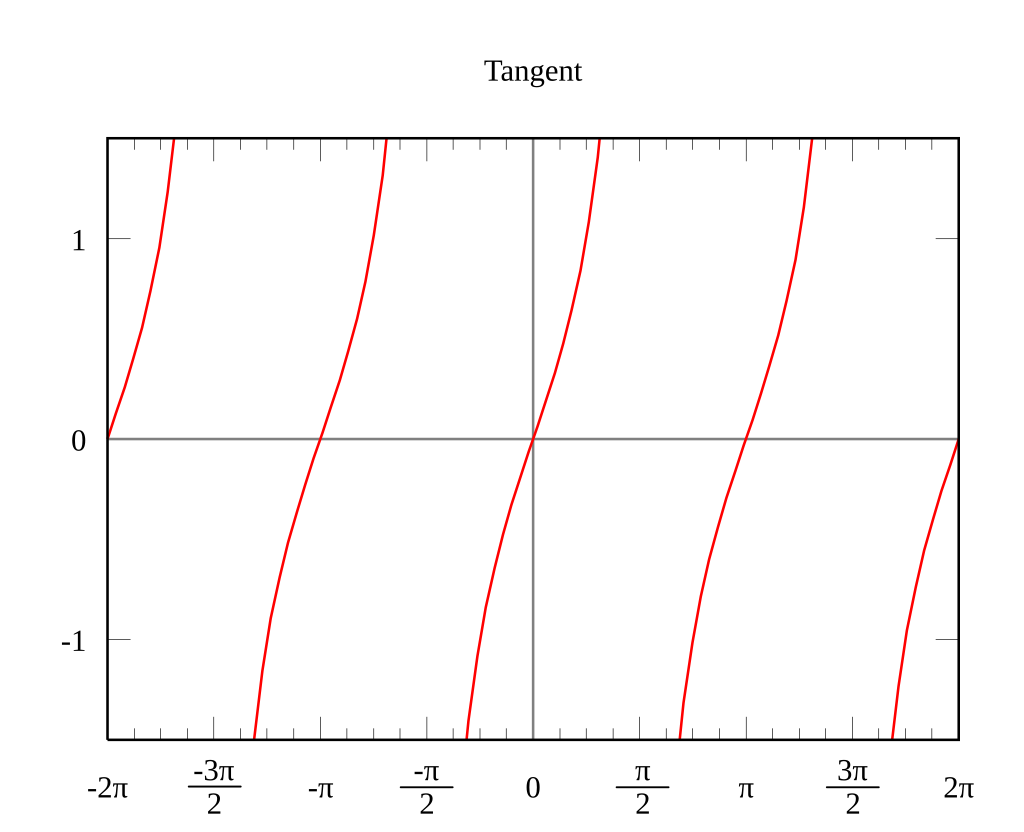
사진출처 - https://ko.wikipedia.org/wiki/%EC%82%BC%EA%B0%81_%ED%95%A8%EC%88%98

삼각함수-1 : https://note.mmmsk.myds.me/Study/%EC%88%98%ED%95%99/%EC%82%BC%EA%B0%81%ED%95%A8%EC%88%98/%EC%82%BC%EA%B0%81%ED%95%A8%EC%88%98-%EA%B8%B0%EB%B3%B8

삼각함수-2 : 

https://designerd.tistory.com/entry/DirectX12-%EC%82%BC%EA%B0%81%ED%95%A8%EC%88%98

Matrix

Vector로 이루어진 직사각형 배열로, 행,m(row), 열,n(column)의 수를 나타냅니다.

3D그래픽스 환경에서 4x4행렬을 사용하여 객체의 Transform관련 변환을 하는데 사용합니다.

2D그래픽스 환경에서는 3x3행렬을 사용하여 객체의 Transform 관련 변환을 하는데 사용합니다.

이번 포스팅에서는 행렬 연산에 대해 알아보겠습니다.

1. 행렬 곱셈

• 두 개의 행렬을 결합하여 새로운 행렬을 생성하는 연산
• 행렬 곱셈 규칙 : A * B
  • B*A와 값이 다르다. (교환 법칙이 성립이 안된다.)
• (앞 행렬의 행의 수) * (뒤 행렬의 열의 수)

2. 대각행렬 (Diagonal Matrix)

• 대각선 이외의 값들을 0으로 설정한다.
• 크기 조절(Scaling)을 할 시 사용한다.

	FMatrix ScaleMatrix = FMatrix(
		FPlane(2.0f, 0.0f, 0.0f, 0.0f),	// X축 Scale
		FPlane(0.0f, 2.0f, 0.0f, 0.0f),	// Y축
		FPlane(0.0f, 0.0f, 2.0f, 0.0f),	// Z축
		FPlane(0.0f, 0.0f, 0.0f, 1.0f)	// Scale 설정, Default = 1.f
	);

	FVector BeforeVector(1.0f, 1.0f, 1.0f);
	FVector ScaledVector = ScaleMatrix.TransformPosition(BeforeVector);

	// 대각 행렬 Matrix 연산 전
	UE_LOG(LogTemp, Log, TEXT("Before Vector : %s"), *BeforeVector.ToString());
	
	// 대각 행렬 Matrix 연산 후
	UE_LOG(LogTemp, Log, TEXT("Scaled Vector : %s"), *ScaledVector.ToString());

3. 단위행렬 (Identity Matrix)

• 변환을 수행하지 않는 기본행렬
• 초기화 시에 사용한다.

	FMatrix IdentityMatrix = FMatrix::Identity;
	
	UE_LOG(LogTemp, Log, TEXT("Identity Matrix : %s"), *IdentityMatrix.ToString());

4. 역행렬 (Inverse Matrix)

• 변환했던 행렬을 반대로 취소하는 데 사용한다.
  • Ex) 특정 위치에서 이동 후 다시 원래 위치로 돌아갈 때

	FMatrix TranslationMatrix = FMatrix::Identity;
	TranslationMatrix = FTranslationMatrix(FVector(10.0f, 0.0f, 0.0f));

	FVector InverseBeforeVector(1.0f, 2.0f, 3.0f);	// 1.0f, 2.0f, 3.0f
	FVector TranslationVector = TranslationMatrix.TransformPosition(InverseBeforeVector); // 11.0f, 2.0f, 3.0f

	// 역행렬
	FMatrix InverseMatrix = TranslationMatrix.Inverse();	// TranslationMatrix의 역행렬
	FVector InverseTranslationVector = InverseMatrix.TransformPosition(TranslationVector);	// 1.0f, 2.0f, 3.0f

	UE_LOG(LogTemp, Log, TEXT("InverseBefore Vector : %s"), *InverseBeforeVector.ToString());
	UE_LOG(LogTemp, Log, TEXT("Translation Vector : %s"), *TranslationVector.ToString());
	UE_LOG(LogTemp, Log, TEXT("InverseTranslation Vector : %s"), *InverseTranslationVector.ToString());

5. 전치행렬 (Transpose Matrix), 직교행렬(Orthogonal Matrix)

• 행과 열을 대각선 축을 기준으로 서로 위치를 바꾼 행렬
• mxn의 전치행렬 : nxm
• 직교행렬 x 전치행렬 = 단위행렬 (전치행렬의 역행렬)

	// 전치행렬
	FMatrix NormalMatrix = FMatrix(
		FPlane(1.0f, 0.0f, 0.0f, 0.0f),
		FPlane(0.0f, 2.0f, 0.0f, 0.0f),
		FPlane(0.0f, 0.0f, 3.0f, 0.0f),
		FPlane(0.0f, 0.0f, 0.0f, 4.0f)
	);

	FMatrix TransposedMatrix = NormalMatrix.GetTransposed();

	FVector NormalVector(1.0f, 2.0f, 3.0f);
	FVector TransposedVector = TransposedMatrix.TransformPosition(NormalVector);

	UE_LOG(LogTemp, Log, TEXT("Normal Vector: %s"), *NormalVector.ToString());
	UE_LOG(LogTemp, Log, TEXT("Transposed Vector: %s"), *TransposedVector.ToString());

6 변환 행렬 (Transformation Matrix)

• 위치, 회전, 크기 조정을 한번에 처리하는 복합  변환을 구현할 때 사용한다.
• Scaling, Rotation, Translation, Relection Matrix
• 각각 x,y,z축을 세타 만큼 회전한다.

	FMatrix TranslationMatrix = FTranslationMatrix(FVector(10.0f, 0.0f, 0.0f));  // X축으로 10만큼 이동
	FRotator Rotation(0.0f, 90.0f, 0.0f);  // Y축으로 90도 회전
	FMatrix RotationMatrix = FRotationMatrix(Rotation);
	FMatrix ScaleMatrix = FMatrix(
		FPlane(2.0f, 0.0f, 0.0f, 0.0f),
		FPlane(0.0f, 2.0f, 0.0f, 0.0f),
		FPlane(0.0f, 0.0f, 2.0f, 0.0f),
		FPlane(0.0f, 0.0f, 0.0f, 1.0f) 
	);

	FMatrix TransformMatrix = TranslationMatrix * RotationMatrix * ScaleMatrix;  // 변환 행렬 결합

	FVector TransBeforeVector(1.0f, 1.0f, 1.0f);
	FVector TransformedVector = TransformMatrix.TransformPosition(TransBeforeVector);

	UE_LOG(LogTemp, Log, TEXT("Transform Before Vector: %s"), *TransBeforeVector.ToString());
	UE_LOG(LogTemp, Log, TEXT("Transformed Vector: %s"), *TransformedVector.ToString());

좌표계

• 공간 상의 위치를 수치적으로 표현하기 위한 체계
• 위치 정의, Transform, 물리적 충돌처리, 렌더링 등을 변환 및 계산할 때 사용한다.
• 2차원 공간과 3차원 공간의 위치를 정의하는 2D좌표계, 3D좌표계
  • 2D : 모니터와 같은 좌표계로 x,y 좌표를 가지고 있다
  • 3D : 3차원 공간에서의 위치를 정의하며 x,y,z좌표를 가지고 있다.
• 직교 좌표계
  • 축들이 서로 직각을 이루는 좌표계
  • Ex) 언리얼 에디터의 기즈모(Gizmo)의 Transform
• 극 좌표계
  • 위치를 각도와 거리로 정의한다.
  • Ex) 항공기의 목적지나 여행방향을 정해주는 항행
• 구면 좌표계
  • 구를 기준으로 한 반지름, 방위각 고도각
  • Ex) 대기 과학, 천문학, 지리학 등 지구나 다른 천체의 표면을 설정할 때

왼손 좌표계

• 왼손의 엄지, 검지, 중지를 각각 X,Y,Z 축 방향으로 펼쳤을 때 벡터의 외적이 정의되는 것.
• Z축이 화면 안쪽으로 향한다.
• 시계 방향으로 회전한다.
• D3DX, 언리얼 엔진이 왼손 좌표계를 사용한다.

오른손 좌표계

• 오른손의 엄지, 검지, 중지를 기준으로 X,Y,Z 축을 방향으로 펼치는 것
• Z축이 화면 바깥쪽으로 향한다.
• 시계 반대 방향으로 회전한다.
• OpenGL, 블렌더 등이 오른손 좌표계를 사용한다.

언리얼에서의 좌표계

좌표계 사이의 변환은 World To View, TranslatedWorld To View처럼 X To Y 형태의 이름으로 표현한다.

월드 좌표계

• 게임 월드의 기준점 (0,0,0)을 기준으로 모든 객체의 위치와 방향이 정의된다.
• 건물, 나무, NPC같은 static한 객체들의 위치 배치
• 플레이어 캐릭터의 위치를 미니맵에 표시

로컬 좌표계

• 특정 객체를 기준으로 상대적인 위치와 방향을 정의한다.
• 캐릭터의 손 위치를 기준으로 무기를 배치
• 차량에서 탑승자 캐릭터의 위치 배치

카메라

• View (CameraSpace)
  • 카메라의 시야 범위를 정의하는 것
  • 카메라의 시야에 따라 객체의 가시성을 판단할 떄 사용한다. (Frustum Space)

스크린

• 모니터 2D화면을 x,y 좌표로 나타낸다.
• 픽셀 단위로 화면상의 위치를 정의한다.
  • UI 또는 HUD를 배치하는데 사용한다.

https://dev.epicgames.com/documentation/ko-kr/unreal-engine/coordinate-system-and-spaces-in-unreal-engine

https://lalyns.tistory.com/entry/%ED%94%84%EB%9F%AC%EC%8A%A4%ED%85%80-%EC%BB%AC%EB%A7%81-%EB%B7%B0%EC%A2%8C%ED%91%9C%EA%B3%84

정의

• 크기와 방향을 가진 수학적 개체
• 2D(x,y), 3D (x,y,z)로 표현한다.
• 단위벡터  - 길이가 1인 벡터
• 영벡터 - 길이가 0인 벡터
• 정규화 - 벡터를 벡터의 길이로 나누어 1로 만든다
• 내적 - 두 벡터가 이루는 각도를 구한다.
• 두 개의 벡터에 수직인 벡터를 구한다.

이동

• 매 시간(Sec)동안 위치 업데이트
  • NewPosition(Vector) = OldPosition(Vector) + (Velocity x DeltaTime)
    • Velocity : 초당 이동 값
    • DeltaTime : 프레임 당 시간(초)
      • Ex) FPS가 60일 경우, DeltaTime = 1/60 (0.01666...)
    • Tick 이벤트 내 Delta Seconds를 사용한 위치 업데이트
• 프레임 기반 이동값
  • NewPosition(Vector) = OldPosition(Vector) + Velocity
    • 프레임 속도에 따라 이동거리가 변동될 수 있다.
    • Tick 이벤트에서 매 프레임 위치 업데이트

단위벡터 (Unit Vector)

• 길이가 1인 벡터
• 벡터가 가르키는 방향을 필요할 때 사용한다.
• 언리얼에서 정규화를 통해 방향을 가져올 수 있다.
  • 블루프린트 : Normalize
  • C++ : GetSafeNormal / GetUnsafeNormal
    • GetSafeNormal : 벡터가 (0,0,0)일 경우, (0,0,0) 반환
    • GetUnsafeNormal : 벡터가 (0,0,0)일 경우, 오류 / 충돌 발생할 수 있다.
• 캐릭터 이동, 카메라 회전, 물리엔진(힘의 방향 또는 충돌 처리)에 사용할 수 있다.

정규화 (Normalization)

• 벡터를 벡터의 길이로 나누어 1로 만드는 것
• 정규화 과정을 거쳐 방향만 남기게 한다
• 본인 * (1 / 본인의 크기)
• 벡터가 (0,0,0)일 경우 정규화가 불가능 하다.

정규화 과정

1. 벡터의 크기 계산

2. 정규화 - 각 성분을 벡터의 크기로 나눈다.

벡터의 내적 (Dot Product)

• 두 벡터가 이루는 각도를 구할 수있다.
• 내적값을 통해 두 벡터 각도의 코사인 값을 구할 수 있다.
• 정규화된 벡터의 내적 값은 -1 ~ 1 사이에 존재한다.
  • Dot > 0 : 두 벡터가 같은 방향
  • Dot < 0 : 두 벡터가 반대 방향
  • Dot = 0 : 두 벡터는 수직
• 언리얼
  • 블루프린트 : Dot Product (V1, V2)
  • C++ : Dot ProDuct (V1, V2)
• 캐릭터 시야각 판별 / 투사체 방향 확인 / 충돌 반사 계산 등에 사용할 수 있다.

내적 공식

벡터의 외적 (Cross Product)

• 두 개의 벡터에 수직인 벡터를 구하는 연산
• 연산값은 크기와 방향을 모두 가지는 벡터값
• A x B = -(B x A)
• A x B = 0
  • A와 B가 평행일 경우
• 두 벡터의 외적 크기 : 두 벡터가 만들 수 있는 평행사변형 넓이
• 두 벡터의 외적 방향 : 오른손 법칙에 따라 방향이 결정된다.
• 언리얼 : CrossProduct(Edge1, Edgw2)
  • FVector Edge1 : Point2 - 1;
  • FVector Edge2 : Point3 - 1;
• 캐릭터의 회전 방향 / 카메라 업벡터 계산 등에 사용한다.

외적 공식

https://designerd.tistory.com/entry/DirectX12-Vector